บทความ
Mathematics
Calculus
เลข 0 จุดเปลี่ยนสำคัญของวงการคณิตศาสตร์!
ลองคิดดูว่า...ตัวเลขที่เราใช้ทุกวัน อย่าง “0” จริง ๆ แล้ว… มนุษย์ใช้เวลากว่า ทำไมเรื่องมันถึงยาวนานขนาดนั้น? คำตอบคือ

โดย Aat Sukavaj
15 ธันวาคม 2568

Engineering
Beam
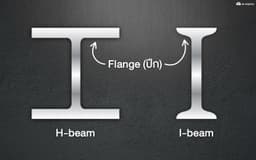
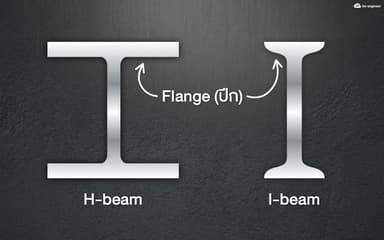
H-beam vs I-beam คานสองชนิดนี้ต่างกันอย่างไร?
คานแบบไหนเรียก H-beam คานแบบไหนเรียก I-beamเมื่อเราพูดถึงงานโครงสร้าง "คาน" หรือ beam คือพระเอกที่ใช้รับน้ำหนักแนวขวาง ทำให้คานเสียหายได้ 2 แบบ คือ
โดย Euw Chaivanon
15 พฤศจิกายน 2568
University
3 กฎทอง “เลือกโปรเจกต์จบ” ให้จบ 4 ปี !
โปรเจกต์จบ หรือ Senior Project สำหรับเด็กวิศวะ คือสนามจริงครั้งแรกในชีวิตนักศึกษาวิศวกรรม.

โดย Aat Sukavaj
1 พฤศจิกายน 2568

Eiffel Tower
Engineering
หอไอเฟล(Eiffel Tower): จุดเปลี่ยนสำคัญของโลกวิศวกรรม
ก่อนที่หอไอเฟลจะถูกสร้างขึ้น โลกวิศวกรรมเคยมี “การค้นพบครั้งยิ่งใหญ่” ที่กลายเป็นพื้นฐานให้กับงานโครงสร้างเกือบทั้งหมดในปัจจุบัน นั่นคือ Beam TheoryBeam Theory ถูกคิดค้นโดยสองนักคณิตศาสตร์–วิศวกรชื่อดัง Leonhard Euler และ Daniel Bernoulli (คนที่เกี่ยวข้องกับค่าคงที่ทางคณิตศาสตร์ e นั่นแหละ)

โดย Euw Chaivanon
27 กันยายน 2568

3 สูตรลับ ที่เด็กวิศวะเกียรตินิยม 90% ใช้เหมือนกันเวลาพูดถึง “เด็กเกียรตินิยม” หลายคนอาจจะนึกถึงคนเก่ง พื้นฐานแน่น สมองดี เรียนอะไรก็เข้าใจเร็ว ซึ่ง…ก็ไม่ผิดทั้งหมด

โดย Aat Sukavaj
9 สิงหาคม 2568

Calculus
Mathematics
ใครเป็นคนคิดแคลคูลัส
ใครเป็นคนคิดแคลคูลัส คำถามที่เป็นประเด็นดราม่าระดับโลกเมื่อ 300 ปีที่แล้ว รู้หรือไม่ว่าแคลคูลัสที่เราเรียนกันในคณะวิศวะเนี่ย มีประวัติการค้นพบที่ดราม่าสุดๆ เพราะมันมีผู้ค้นพบพร้อมกันถึง 2 คน!

โดย Aat Sukavaj
25 พฤษภาคม 2568

Engineering
วิศวกรรมเเต่ละสาขา เรียนเกี่ยวกับอะไร?
1. วิศวกรรมเครื่องกล (Mechanical Engineering) 2. วิศวกรรมโยธา (Civil Engineering)

โดย Euw Chaivanon
25 เมษายน 2568

3 สิ่งที่อยากฝากถึงน้องๆที่กำลังจะเรียนมหาลัย(จากรุ่นพี่ที่เคยผ่านมันมาแล้ว)

โดย Aat Sukavaj
20 เมษายน 2568

Experience
Engineering
จากเด็กม.ปลายเกรดน้อย สู่การจบวิศวะแบบติด TOP ของรุ่น
มาฟังเทคนิคการเปลี่ยนมุมมองการเรียน...ด้วยประสบการณ์ตรงจากติวเตอร์พี่จุ๊ ของเรากันครับ .

โดย Aat Sukavaj
13 เมษายน 2568

Civil Engineering
ใครคือวิศวกรโยธา คนเเรกในประวัติศาสตร์
พีระมิด สิ่งก่อสร้างที่ถูกจัดว่าเป็น 1 ใน 7 สิ่งมหัศจรรย์ของโลกยุคโบราณที่ถูกสร้างมาแล้วกว่า 2,600 ปีก่อนคริสต์กาล และชายที่ออกแบบพีระมิดขั้นบันไดแห่งซักการา (Step Pyramid of Saqqara) เป็นแห่งแรกของโลก คือ อิมโฮเทป (Imhotep)ในปัจจุบันโลกของเรามีสิ่งปลูกสร้างมากมายหลายอย่างให้เราได้เห็นเเละสัมผัส ทั้งสิ่งโบราณเเละทันสมัย ล้วนเเล้วเกิดจากการออกเเบบของเหล่าวิศวกรโยธาทั้งสิ้น เเละในวันนี้จะพาทุกคนมาพบกับวิศวกรโยธาคนเเรกในประวัติศาสตร์

โดย Euw Chaivanon
7 เมษายน 2568
